‘Clustering’ Australia’s Patent Applicants

I recently generated an interactive map of Australia’s most innovative postcodes, using recent Australian patent application and maintenance data.  While it is, of course, interesting to know whether one lives or works in a particularly innovative part of the country, the exercise of classifying activity by postcode is inherently artificial, in that it presupposes there is something ‘meaningful’ about the region covered by each particular postcode.  There is, however, no reason to suppose that this is the case.  There is nothing about the boundaries between adjacent postcodes, which are set by postal authorities for their own administrative purposes, that would necessarily lead to them being well-suited to the task of locating innovative activity.

A somewhat less arbitrary regional structure (from a socio-economic perspective) is defined by the Australian Bureau of Statistics (ABS), in the form of a hierarchy of ‘statistical areas’ (SAs).  In conjunction with its Australian Geography of Innovative Entrepreneurship (2015) research paper, the Department of Industry, Innovation and Science produced its own interactive Innovation Map using the ABS SA3 definitions as the basic regional unit.  Generally speaking, SA3s are regions with populations between 30,000 and 130,000 persons and reflecting regional identity in terms of geographic and socio-economic characteristics.  This results in aggregation of data over wider areas than individual postcodes.  In Sydney, for example, it results in the greatest number of patent filings being attributed to the Sydney Inner City SA3 region.  It is not possible, at this level, to observe the particular concentration of activity occurring around Macquarie University in the North of Sydney noted in my postcode-based analysis, since this is ‘diluted’ by lower activity in other parts of the encompassing Ryde-Hunters Hill SA3 region.

The answer you receive thus depends upon the question you ask, e.g. how many patent applicants are located within a particular postcode, or within a particular SA3 region?  In both of these cases, a set of geographic areas is imposed before even commencing the analysis, and the results are constrained by this choice.  In the real world, however, innovation does not begin or end at some artificial boundary set by a postal officer or statistician.  So how can we analyse the distribution of patent applicants objectively and without applying predetermined geographic constraints?

One approach to this problem is a technique known as cluster analysis, or clustering.  The idea behind clustering is to apply an algorithm to automatically group elements in a data set according to a measure of similarity, such as geographic proximity.  It can be regarded as a form of machine learning in which the algorithm is designed to ‘discover’ patterns in the data without explicit direction from a human operator. 

In this article, I present some results of applying one of the most commonly-used clustering algorithms, k-means, to an Australian patent application data set to analyse national and local distributions of patent applicants.  This kind of analysis could be used, for example, to identify regions in which it could be most productive to invest in support for innovative industries, or to set up a business providing services to innovative companies, such as R&D tax advice or IP services.

The Data Set

For this exercise I started with the same data set I used in my postcode analysis, i.e. ‘active’ Australian users of the patent system, based upon recent filings and/or applications and patents that are being actively maintained, drawing on the publicly-available Intellectual Property Government Open Data (IPGOD) 2016 data.  However, in this case I did not include provisional filings, which I found had no significant impact on the overall geographical distribution of applicants.  I also limited the sample to applicants for which I have location data with precision greater than the postcode level, to avoid creating artificial clusters of applicants at post offices!  This left me with a total of 8228 active users (applicants and patent owners) Australia-wide, as of the end of 2015.

Algorithms – k-means and Silhouettes

The k-means algorithm attempts to find a fixed number, k, of local ‘centres’, each of which is assigned to a corresponding cluster of data points, such that the overall average (or total) distance between each data point and its associated centre is minimised.  The basic algorithm requires k to be set in advance, which raises the question of how to choose the number of centres around which the data will be clustered.  After all, the primary objective of the exercise is to identify regions of filing activity without imposing preconceived ideas of how many regions there may be, or where they are located.

To address this problem, it is necessary to try a number of different values of k and identify which one gives the ‘best’ clustering result, according to some reasonable criterion.  For this, I used a method known as Silhouettes, which measures how ‘similar’ a data point is to those in its own cluster, as compared to those in other (primarily neighbouring) clusters.  Silhouette values range between -1 to 1, with higher values being better.  In all cases the algorithm was able to find a value of k for which the average Silhouette value was a maximum, i.e. where any smaller or larger values of k would produce an inferior result according to this metric.

I weighted each applicant location according to the number of applications/patents associated with that applicant, i.e. the algorithm operated according to a ‘one vote per application’ principle, rather than ‘one vote per applicant’.

National Clusters

I first ran the above algorithm using the complete data set, across the entirety of Australia.  The results are shown in the (non-interactive) map below, where applicant locations are colour-coded to show each cluster identified by the algorithm.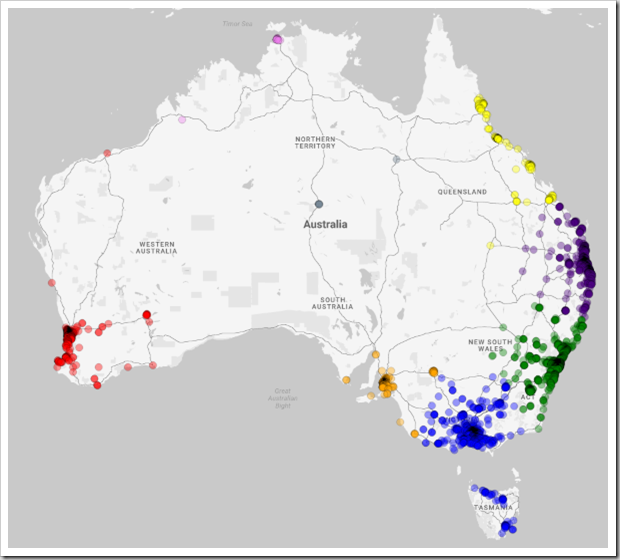

The algorithm identified eight clusters in this case.  Unsurprisingly, five of these include the state capitals Sydney, Melbourne, Brisbane, Perth, Adelaide, and Darwin (shown in green, blue, indigo, red, orange, and pink respectively).  More interestingly, northern Queensland has been identified as home to a cluster in its own right (shown in yellow).  On the other hand, the density of applications from Tasmania proved insufficient to qualify as a distinct cluster, instead ending up lumped-in with the Melbourne and regional Victorian applicants, in blue.  Finally, if you look very carefully you will see a couple of grey circles, making up a tiny central Australian cluster.  (It is worth noting that the difference in Silhouette value between this result, and an alternative seven-cluster solution having the central points clustered with the northern applicants in pink, is only around 0.1%.)

Regional Clusters – Brisbane Area

I have also extracted all of the applicants within a 150 km radius of the Brisbane GPO from the complete data set, and run the algorithm again on this subset.  The results are shown in the map below (which this time is interactive, so you can pan and zoom to view additional detail).

Here, four clusters have been identified: the Brisbane metropolitan area (blue); the Sunshine Coast to the north (green); the Gold Coast to the south (red); and Toowoomba to the west (indigo).  At this regional scale, these are all quite distinct clusters of commercial activity, associated with corresponding population centres, although this was not apparent in the data when analysed at the national scale.

It is interesting to compare this with the ‘heat map’ in my earlier postcode-based analysis – if you zoom in on the Brisbane area until it resolves into a distinct ‘hot spot’, and then pan north, south, and west, the same pattern of clusters emerges.  In the present case, however, the algorithm has discovered these clusters of its own accord, without any human guidance or intervention, which I find quite fascinating!

Conclusion – Different Techniques, Different Insights

Over a couple of articles I have illustrated different ways to analyse Australian geographical patent application data.  Firstly, I mapped patenting activity to postcodes, and was thereby able to identify specific localities of innovation, particularly in and around universities and research institutes.  The Australian Government’s Department of Industry, Innovation and Science has generated a similar interactive map based upon larger socio-economic regions, providing a lower-resolution view of activity.

The heat mapping technique employed in the postcode-based analysis also enables wider regions of more intensive patenting activity to be explored and identified by visual inspection.  However, in the current article I have demonstrated that machine learning techniques, and specifically the k-means clustering algorithm, can be employed to discover similar characteristics in the data without human intervention.  While such techniques obviously have their own limitations, they have the distinct advantage of objectivity, and the potential to reveal patterns that a human operator might miss, or that may be impossible to identify in the results of an analysis that presupposes certain characteristics, such as an association between patenting intensity and postcode or socio-economic regions.

In practice, it will often be necessary to apply a variety of techniques, using different parameters, in order to maximise the insights gained from available data.

Tags: Australia, Innovation, IPGOD, Patent analytics